浅析数据结构-图论之Floyd算法
定义:
Floyd算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,与Dijkstra算法类似。(定义摘自百度)
简单来说,这个算法来解决的任意两点之间的最短路径,它可以正确地处理向图的最短路径问题或有向图或者负权重(但是可以不存在负权重循环)。
由于该算法设计到动态规划的一些思想,所以笔者在思考某个问题的时候,并没有联想到到这个算法的本质,当然这是后话了。
分析问题
闲话少叙,开始正题。
给出以下一个有向图(图片来自网络,太难画了)。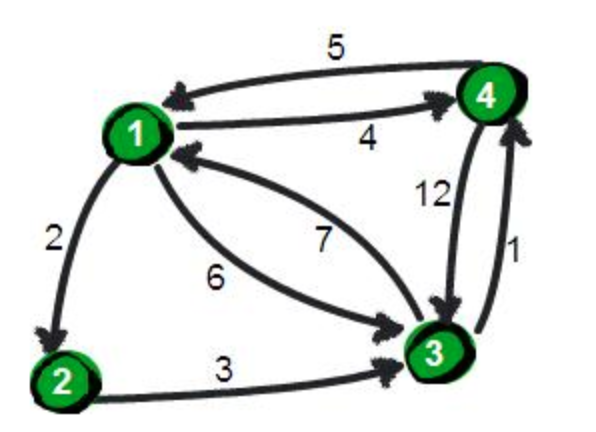
这时候我们来思考一个问题:在这个有向图中,我想从 1 点到达到 3 点,有几种方式,几种方式到路程怎么样?
- 从 1 可以直接到达 3 点,距离为6;
- 从 1 路过 2 号点,最后到达 3 点,距离是5;
- 从 1 路过 4 号点,最后到达 3 点,距离是16;
- 其他有关于多走几次回路的方式,就不再赘述。
经过上面的分析,我们发现从 1 号点到达 3 号点,以经过 2 号点的方式距离最短。这时候我们来回顾摘自百度的有关Floyd算法的定义:Floyd算法又称为插点法,这个 2 号点就是定义所说点有关插点的解释了。也就是说,我们在路过其他点到达目的地的时候,往往会有奇效。
这时候问题来了,从 1 号点到达 3 号点我们可以通过观察,轻易的写出老,那么所有的点到所有到点呢?这个案例扩充到N个点呢?很明显。仅通过肉眼观察是很难做到的。这时候必须通过计算机来解决此问题。
我们继续分析这个问题,通过特例完成通解。
我们来想一想,如果要让任意两点(例如从顶点a点到顶点b)之间的距离变短,只能引入第三个点(顶点k),并通过这个顶点k中转即a->k->b,才可能缩短原来从顶点a点到顶点b的距离。那么这个中转的顶点k是1~n中的哪个点呢?甚至有时候不只通过一个点,而是经过两个点或者更多点中转会更短,即a->k1->k2b->或者a->k1->k2…->k->i…->b。
分析有向图,必不可少的工具,就是 邻接矩阵 ,我们来画出上述有向图的邻接矩阵。
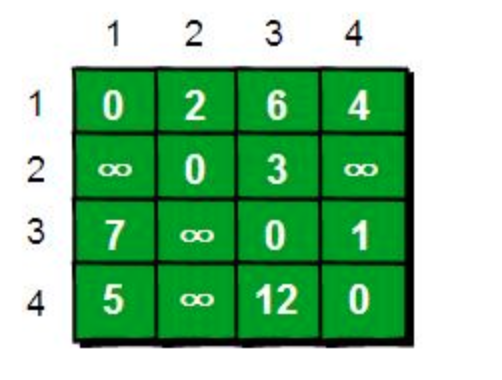
有向图,任意点到任意点本身到距离是0,没有直接通路的情况下,把距离记作 ∞ 。
逐渐深入问题
假定,我们只能路过 1 号点来作为中转点,这时候我们来求一下,各个点到各个点的最短距离。也就是说,如果两点之间直接距离与经过 1 号点点距离做比价,找出最短点距离;如果没有直接通路,则能通过 1 点能连通,那便是此条路为最短路径。
那我们应该如何求呢?我们把 i 点到 j 的距离记作e[i] [j]。只需判断e[i] [1] + e[1] [j]是否比e[i] [j]要小即可。e[i] [1]+e[1] [j]表示的是从 i 号顶点先到 1 号顶点,再从 1 号顶点到 j 号顶点的路程之和。其中 i 是1–n循环,j 也是1–n循环,代码实现如下:
1 | for (i = 1; i <= n; i++){ |
在只允许经过1号顶点的情况下,任意两点之间的最短路程更新为: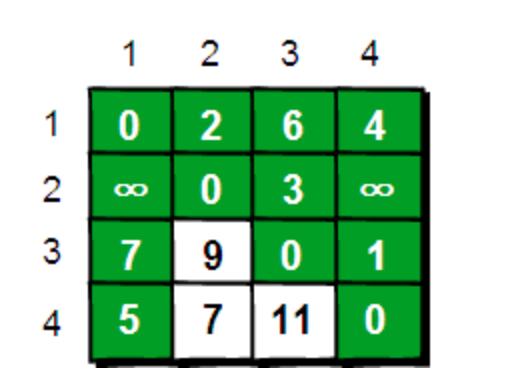
我们继续思考问题:如果规定,只允许经过 1 号点和 2 号点,这时候各个点相互之间点距离怎么样又是怎么样的呢!?代码如下图所示:
1 | for (i = 1; i <= n; i++){ |
我们来看一下计算的结果:
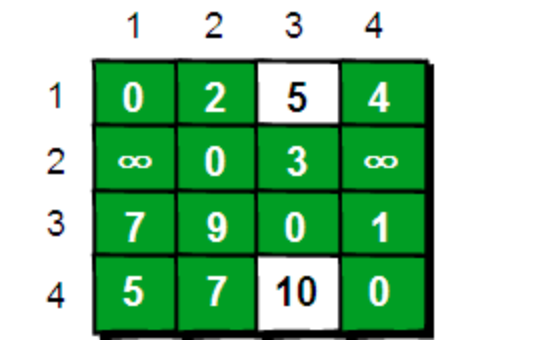
在相比只允许通过1号顶点进行中转的情况下,这里允许通过1和2号顶点进行中转,使得e[1] [3]和e[4] [3]的路程变得更短了。
这时候不难发现,当要求只允许经过经过 1 – n 的时候,我们的算法可以这样书写:
1 | for (i = 1; i <= n; i++){ |
然而,这样并不能解决实际问题,如果 1 到 2 点经过两个点的时候比只经过一个点距离更小时,不就是不满足最短路径的需求了吗?
不着急,这时候算法还是五步,三层for循环,我们只需要这样做:
1 | for (k = 1; k <= n; k++){ |
至此,算法的核心代码已经说完了,现在有一个小小的问题:请问无穷大在代码里怎么表示呢?应该会有人说,不就是 int MAX = 99999999;吗?其实int型的无穷大,我们可以经常这么表示 int MAX = 0x3f3f3f; 至于为什么,就留给读者自行思考了,笔者就不再赘述了。
注意 :不是所有的有向图都是正权边的,Floyd不适合带有 负权回路 的有向图,这样是没有最短路径的。
再深入思考
下面再看一个题目:
这一题,便可套用Floyd算法,虽然不是直接求得题目得解,使用此算法算是一种曲线救国的解法。读者可以自己动手试试。