04_浅析数据结构-线性结构之线性表

浅析数据结构-线性结构之线性表

线性结构的特点：

• ① 存在一个唯一的被称为“第一个”的数据元素；
• ② 存在一个唯一的被称为“最后一个”的数据元素；
• ③ 除第一个元素外，每个元素均有唯一一个直接前驱；
• ④ 除最后一个元素外，每个元素均有唯一一个直接后继。

线性表：是由n(n≧0)个数据元素(结点)a1，a2， …an组成的有限序列。该序列中的所有结点具有相同的数据类型。其中数据元素的个数n称为线性表的长度。
当n=0时，称为空表。
当n>0时，将非空的线性表记作： (a1，a2，…an)
a1称为线性表的第一个(首)结点，an称为线性表的最后一个(尾)结点。
a1，a2，…ai-1都是ai(2≦i≦n)的前驱，其中ai-1是ai的直接前驱;
ai+1，ai+2，…an都是ai(1≦i ≦n-1)的后继，其中ai+1是ai的直接后继。

注：一个数据元素可以由若干个数据项组成。在这情况下，常把数据元素称为记录，含有大量记录的线性表称为文件。

线性表的表示与实现

• a.顺序存储[数组]

顺序存储 ：[数组]把线性表的结点按逻辑顺序依次存放在一组地址连续的存储单元里。用这种方法存储的线性表简称顺序表。

• ①什么是数组？
  元素类型相同，大小相等。
• ②数组的优缺点：
  • 优点：
    1、按照索引查询元素速度快
    2、能存储大量数据
    3、按照索引遍历数组方便
  • 缺点：
    1、根据内容查找元素速度慢
    2、数组的大小一经确定不能改变。
    3、数组只能存储一种类型的数据
    4、增加、删除元素效率慢
    5、未封装任何方法，所有操作都需要用户自己定义。

/*
1、CreatList(SqList &L,int n) 
参数：顺序表L，顺序表长度n 功能：创建长度为的顺序表 时间复杂度：O(n)
2、InitList(SqList &L) 
参数：顺序表L 功能：初始化 时间复杂度:O(1)
3、InsertList(SqList &L,int i,ElemType e) 
参数:顺序表L,位置i,元素e 功能：位置i处插入元素e 时间复杂度:O(n)
4、ListDelete(SqList &L,int i) 
参数:顺序表L,位置i 功能：删除位置i处元素 时间复杂度:O(n)
5、LocateElem(SqList L,ElemType e) 
参数:顺序表L,元素e 功能：返回第一个等于e的元素的位置 时间复杂度:O(n)
6、PrintList(SqList L) 
参数:顺序表L 功能：遍历L，并输出
*/
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#define MaxSize 100
#define ElemType int
#define Status int
using namespace std;
//顺序表数据结构
typedef struct
{
  ElemType data[MaxSize];//顺序表元素
  int length;            //顺序表当前长度
}SqList;
//************************基本操作函数****************************//
//初始化顺序表函数，构造一个空的顺序表 
Status InitList(SqList &L)
{
  memset(L.data, 0, sizeof(L));//初始化数据为0
  L.length = 0;                //初始化长度为0
  return 0;
}
//创建顺序表函数 初始化前n个数据
bool CreatList(SqList &L, int n)
{
  if (n<0 || n>MaxSize)false;//n非法
  for (int i = 0; i<n; i++)
  {
    int temp;
    scanf("%d", &L.data[i]);
    L.length++;
  }
  return true;
}
//插入函数 位置i插入数据 i及之后元素后移  1=<i<=length+1 
bool InsertList(SqList &L, int i, ElemType e)
{
  if (i<1 || i>L.length + 1) //判断位置是否有效
  {
    printf("位置无效！！！\n");
    return false;
  }
  if (L.length >= MaxSize)//判断存储空间是否已满
  {
    printf("当前存储空间已满！！！\n");
    return false;
  }
  for (int j = L.length; j >= i; j--)//位置i及之后元素后移
  {
    L.data[j] = L.data[j - 1];
  }
  L.data[i - 1] = e;
  L.length++;
  return true;
}
//删除函数 删除位置i的元素 i之后的元素依次前移
bool  ListDelete(SqList &L, int i)
{
  if (i<1 || i>L.length)
  {
    printf("位置无效！！！\n");
    return false;
  }
  for (int j = i; j <= L.length - 1; j++)//位置i之后元素依次前移覆盖
  {
    L.data[j - 1] = L.data[j];
  }
  L.length--;
  return true;
}
//查找函数 按位置从小到大查找第一个值等于e的元素 并返回位置
int LocateElem(SqList L, ElemType e)
{
  for (int i = 0; i<L.length; i++)//从低位置查找
  {
    if (L.data[i] == e)
      return i + 1;
  }
  return 0;
}
//倒置函数 将原顺序表直接倒置
void Reverse(SqList &L)
{
  if (L.length)
    for (int i = 0; i<L.length - 1 - i; i++)
    {
      int t = L.data[i];
      L.data[i] = L.data[L.length - 1 - i];
      L.data[L.length - 1 - i] = t;
    }
}
//***************************功能函数***********************************//
//输出功能函数 按位置从小到大输出顺序表所有元素
void PrintList(SqList L)
{
  printf("当前顺序表所有元素:");
  for (int i = 0; i<L.length; i++)
  {
    printf("%d ", L.data[i]);
  }
  printf("\n");
}
//创建顺序表函数
void Create(SqList &L)
{
  int n; bool flag;
  L.length = 0;
  printf("请输入要创建的顺序表长度(>1):");
  scanf("%d", &n);
  printf("请输入%d个数（空格隔开）:", n);
  flag = CreatList(L, n);
  if (flag) {
    printf("创建成功！\n");
    PrintList(L);
  }
    else printf("输入长度非法！\n"); 
}
//插入功能函数 调用InsertList完成顺序表元素插入 
//调用PrintList函数显示插入成功后的结果
void Insert(SqList &L)
{
  int place; ElemType e; bool flag;
  printf("请输入要插入的位置(从1开始)及元素:\n");
  scanf("%d%d", &place, &e);
  flag = InsertList(L, place, e);
  if (flag)
  {
    printf("插入成功！！！\n");
    PrintList(L);
  }
}
//删除功能函数 调用ListDelete函数完成顺序表的删除 
//调用PrintList函数显示插入成功后的结果
void Delete(SqList &L)
{
  int place; bool flag;
  printf("请输入要删除的位置(从1开始):\n");
  scanf("%d", &place);
  flag = ListDelete(L, place);
  if (flag)
  {
    printf("删除成功！！！\n");
    PrintList(L);
  }
}
//查找功能函数 调用LocateElem查找元素
void Search(SqList L)
{
  ElemType e; int flag;
  printf("请输入要查找的值:\n");
  scanf("%d", &e);
  flag = LocateElem(L, e);
  if (flag)
  {
    printf("该元素位置为:%d\n", flag);
  }
  else
    printf("未找到该元素！\n");
}
//菜单
void menu()
{
  printf("********1.创建    2.插入*********\n");
  printf("********3.删除    4.查找*********\n");
  printf("********5.倒置    6.输出*********\n");
  printf("********7.退出    *****************");
}
int main()
{
  SqList L; int choice;
  InitList(L);
  while (1)
  {
    menu();
    printf("请输入菜单序号：\n");
    scanf("%d", &choice);
    if (7 == choice) break;
    switch (choice)
    {
      case 1:Create(L); break;
      case 2:Insert(L); break;
      case 3:Delete(L); break;
      case 4:Search(L); break;
      case 5:Reverse(L); break;
      case 6:PrintList(L); break;
      default:printf("输入错误！！！\n");
    }
  }
  return 0;
}

g++和CLion，运行界面：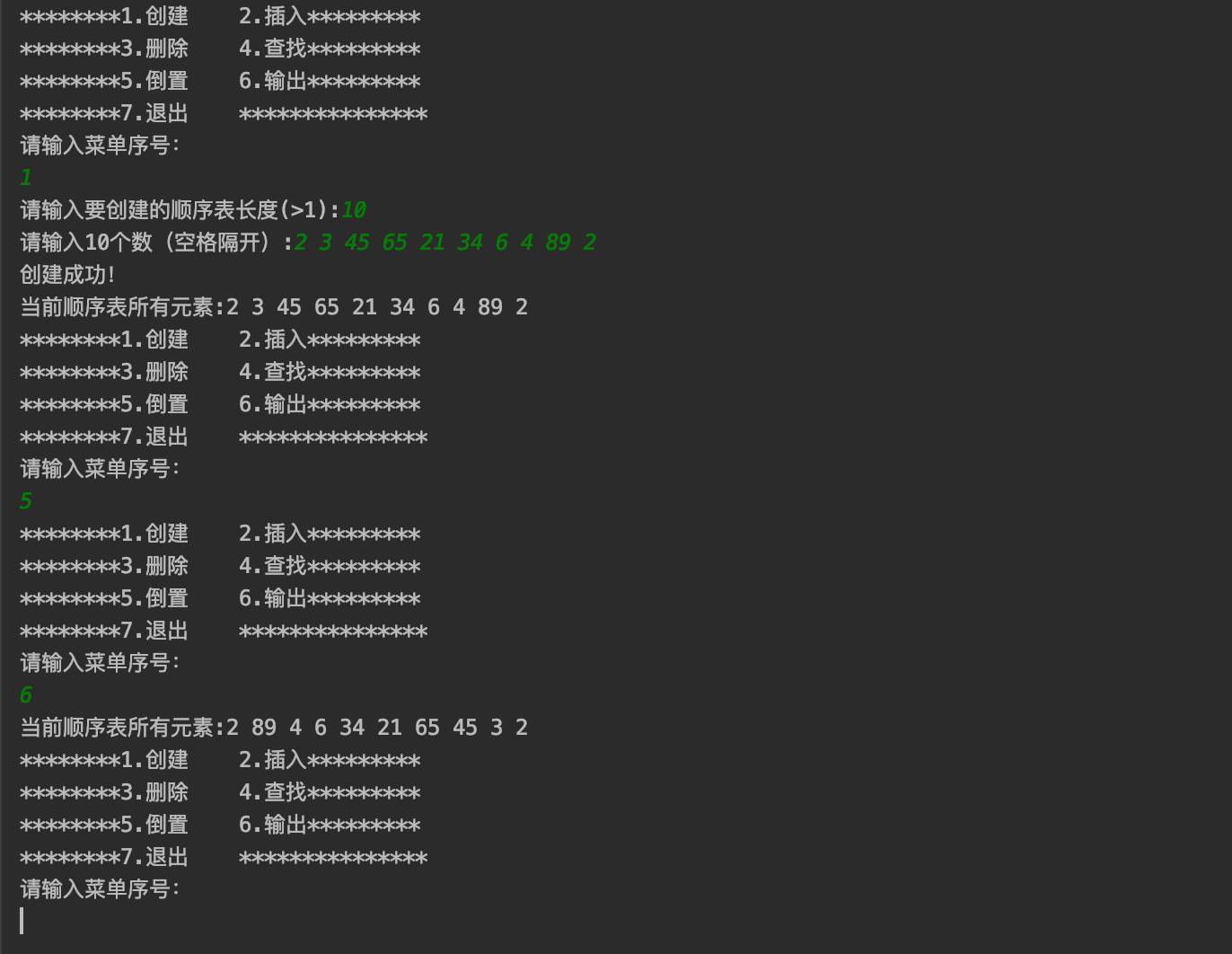

这种写法是所见的大多的写法，个人认为这种写法稍欠些想法，在结构体中为什么要直接放入一个数组呢？我们是不是可以这么写：

typedef struct
{
  ElemType *data;	//顺序表元素
  int length;		//顺序表当前长度
  int nLength;		//顺序表的有效长度
}SqList;

然后在在生成顺序表的时候，给ElemType *data赋值空间，类似于这么写：

//nLength为用户手动输入的有效元素的个数
ElemType* data = (ElemType*)malloc(sizeof(ElemType) * nLength);

看过书的同学看到这就明白了，这种写法就是严奶奶书上的写法。笔者稍微手写试了一下。还有一些完善的地方，读者可自行修改。过于简单，注释就不写了。

#include <iostream>
#include <cstdlib>
using namespace std;
typedef int ElemType;
typedef struct Node {
    //数组第一个元素的地址
    ElemType *elem;
    //数组能容纳最大元素的个数
    int length;
    //当前数组元素有效个数
    int cnt;
}Sqlist,*SqlList;
void Listinit(SqlList L,int length) {
    L->elem = (ElemType *)malloc(length * sizeof(ElemType));
    if(NULL == L->elem) {
        cout << "动态内存分配失败！" << endl;
        exit(-1);
    } else {
        L->length = length;
        L->cnt = 0;
    }
    return;
}
bool is_Listempty(SqlList L) {
    return (0 == L->cnt);
}
bool is_Listfull(SqlList L) {
    return L->cnt == L->length;
}
bool ListInsert(SqlList L,int pos,int val) {
    if(is_Listfull(L))
        return false;
    int i;
    if(pos < 1 || pos > L->cnt + 1)
        return false;
    for(i = L->cnt - 1;i >= pos - 1;--i) {
        L->elem[i + 1] = L->elem[i];
    }
    L->elem[pos - 1] = val;
    ++L->cnt;
    return true;
}
bool ListDelete(SqlList L,int pos,int *pval) {
    if(is_Listempty(L))
        return false;
    int i;
    if(pos < 1 || pos > L->cnt)
        return false;
    for(i = pos;i < L->cnt;++i) {
        L->elem[i + 1] = L->elem[i];
    }
    --L->cnt;
    return true;
}
void Reverse(SqlList L) {
    if(L->cnt) {
        int i = 0;
        int j = L->cnt - 1;
        while(i < j) {
            L->elem[i] = L->elem[i] ^ L->elem[j];
            L->elem[j] = L->elem[i] ^ L->elem[j];
            L->elem[i] = L->elem[i] ^ L->elem[j];
            ++i;
            --j;
        }
        return;
    }
}
void ListPrint(SqlList L) {
    if(is_Listempty(L))
        cout << "数组为空！" << endl;
    else{
        cout << "数组有效个数：" << L->cnt << endl;
        for(int i = 0;i < L->cnt;++i)
            cout << L->elem[i] << " ";
        cout << endl;
    }
}
int main(){
    ElemType data;
    Sqlist L;
    Listinit(&L,10);
    ListInsert(&L,1,50);
    ListInsert(&L,2,60);
    ListInsert(&L,3,70);
    ListPrint(&L);
    ListDelete(&L,2,&data);
    Reverse(&L);
    ListPrint(&L);
    return 0;
}

时间复杂度分析
时间主要耗费在数据元素的比较和移动操作上。
首先，在线性表L中查找值为x的结点是否存在;
其次，若值为x的结点存在，且在线性表L中的位置为i ，则在线性表L中删除第i个元素。
设在线性表L删除数据元素概率为Pi，不失一般性，设各个位置是等概率，则Pi=1/n。
◆ 比较的平均次数： Ecompare=∑pi * i (1≦i≦n)
∴ Ecompare=(n+1)/2 。
◆ 删除时平均移动次数：Edelete=∑pi * (n-i) (1≦i≦n)
∴ Edelete=(n-1)/2 。 平均时间复杂度：Ecompare+Edelete=n ，即为O(n)